Bernoulli’s Equation

[Audio] Hi everyone Today our topic is Bernoulli's equation.

[Audio] Bernoulli's equation is the fundamental equation in fluid dynamics that relates pressure to fluid speed and height. Bernoulli's equation is the consequence of the Law of conservation of energy..

[Audio] CHARACTERISTIC OF IDEAL FLUID: The fluid is non-viscous In non-viscous fluid, internal friction is neglected. The fluid is steady The flow is laminar, and the velocity of the fluid at each point remains constant. The fluid is incompressible The density of incompressible fluid is constant. The fluid is irrotational The fluid has no angular momentum at about any point. The temperature does not vary Phenomena such as convection of fluids in which liquid is heated at bottom of the vessel, cools, rises are not considered.

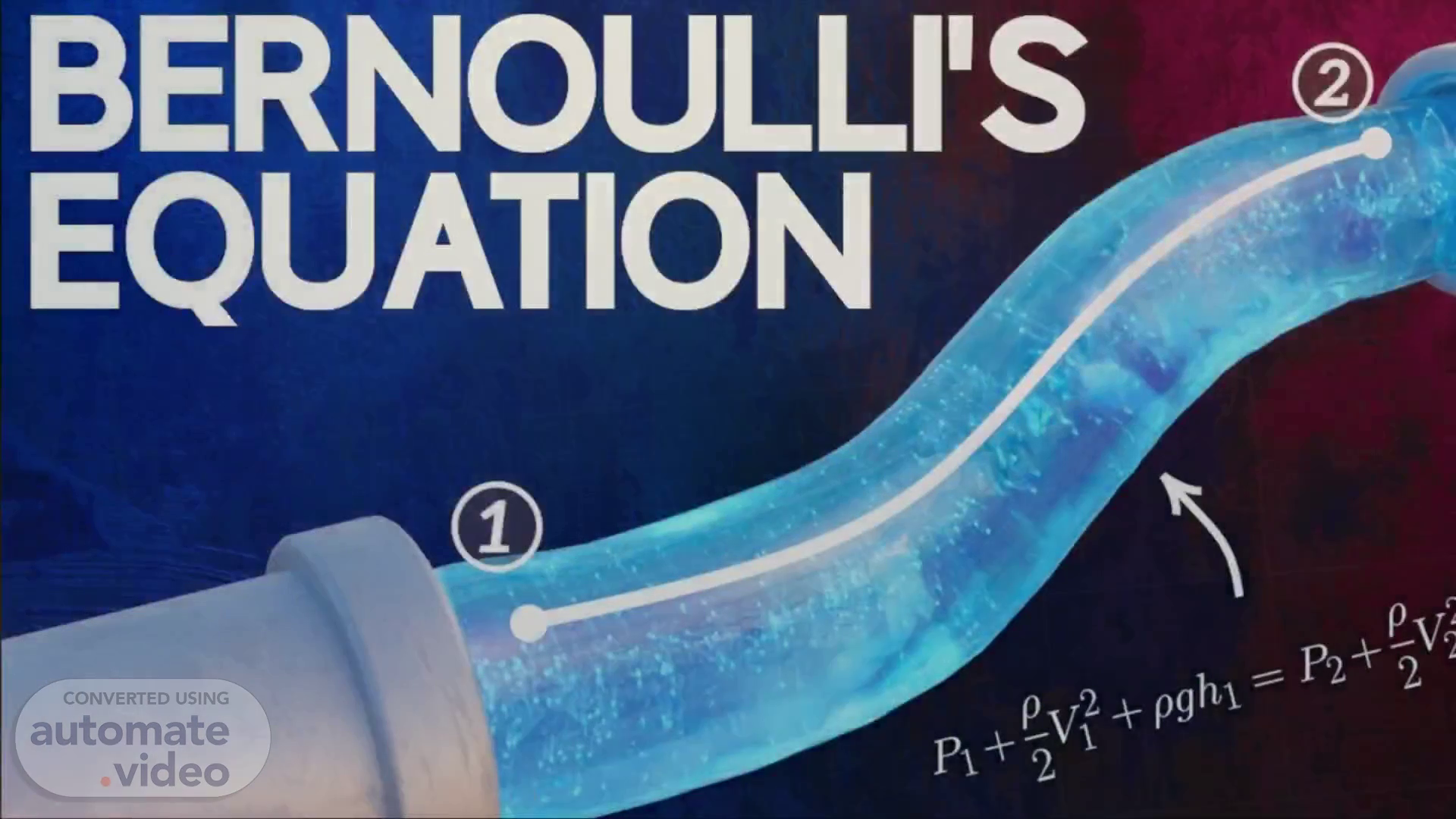
[Audio] In deriving Bernoulli's equation Consider an ideal fluid that is incompressible Non viscous and flows in a steady state through a pipe of Non uniform size as shown in the figure let v one and p one is the pressure and velocity of fluid at lower end of height h one Similarly v two and p two be the pressure and velocity of fluid at height h two The work done in lower end of pipe is W equal to f one d one cos theta Where theta equal to zero So work done equal to F one delta x one Where delta x one is the displacement of fluid at lower end.

[Audio] The pressure exerted on lower end of pipe is Pressure equal to force exerted per unit area Where f one equal to p one A one So work done becomes W one equal to p one A one delta x one By definition of density Density equal to mass per unit volume Volume equal to mass by density A one and delta x one equal to volume of fluid so replacing V A one delta x one equal to delta m one by rho The work done at lower end of pipe is W one equal to p one delta m one by rho.

[Audio] Similarly word done at upper end of pipe is W two equal to negative of p two delta m two by rho The negative sign tell us force and displacement are opposite to each other. The total work done equal to sum of all work done W equal to p one delta m one by rho minus p two delta m two by rho.

[Audio] The net change in kinetic energy One by two delta m two v two square minus one by two delta m one v one square The net change in potential energy Delta m two g h two minus delta m one g h one According to law of conservation of energy Work done equal to sum of its energy Putting values we get P one delta m one by rho minus p two delta m two by rho equal to Half delta m two v two square minus half delta m one v one square plus delta m two g h two minus delta m one g h one For ideal fluid equal mass should flow across both ends So delta m two equal to delta m one equal to delta m So above equation becomes.

[Audio] Taking common delta m by rho and we get P one minus p two equal to Half rho v two square minus half rho v one square plus rho g h two minus rho g h one Rearranging the above equation we get Bernoulli's equation P plus half rho v square plus rho g h equal to constant. This equation is the equation of continunity.

[Audio] Thanks for watching us.. Thanks for watching us.